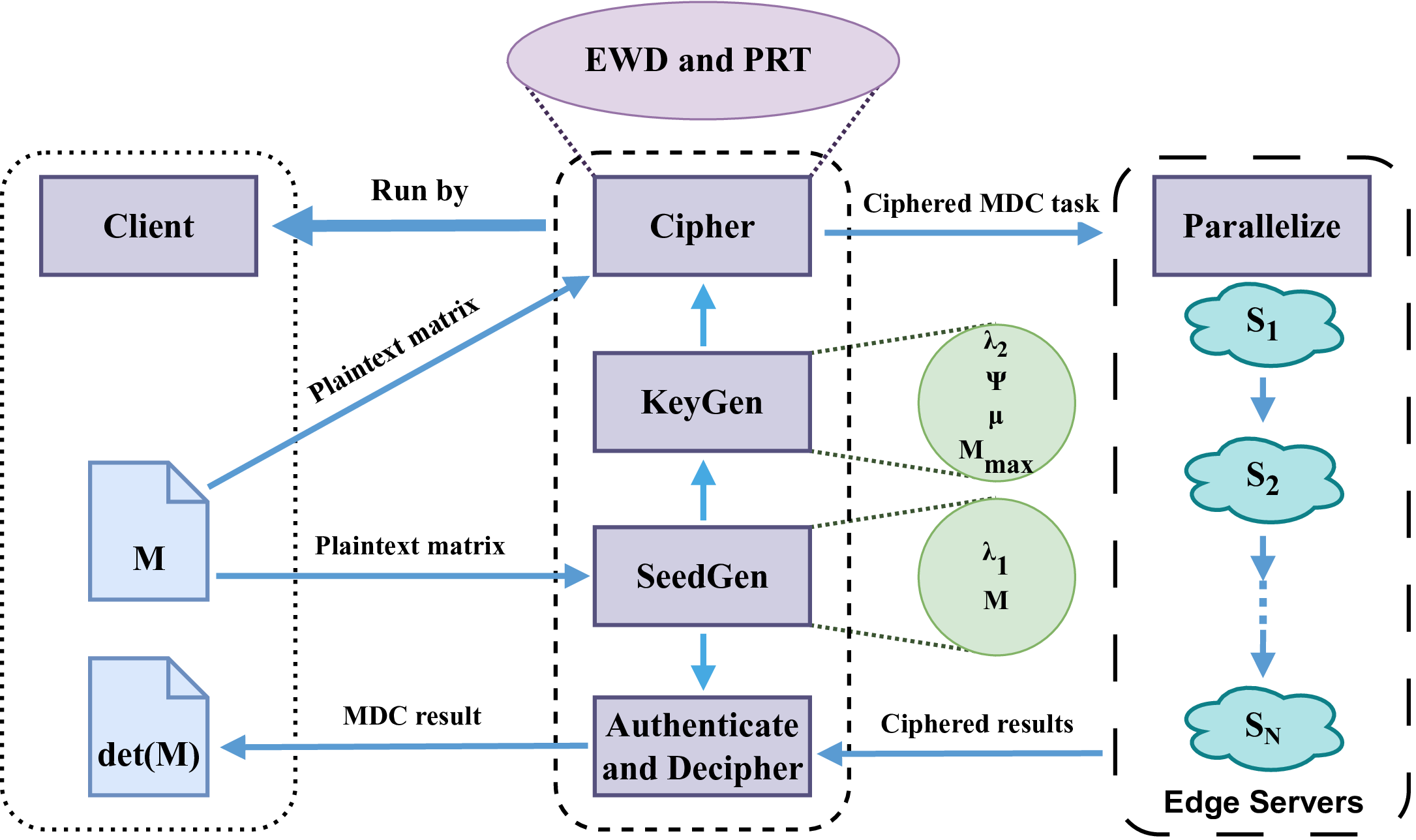
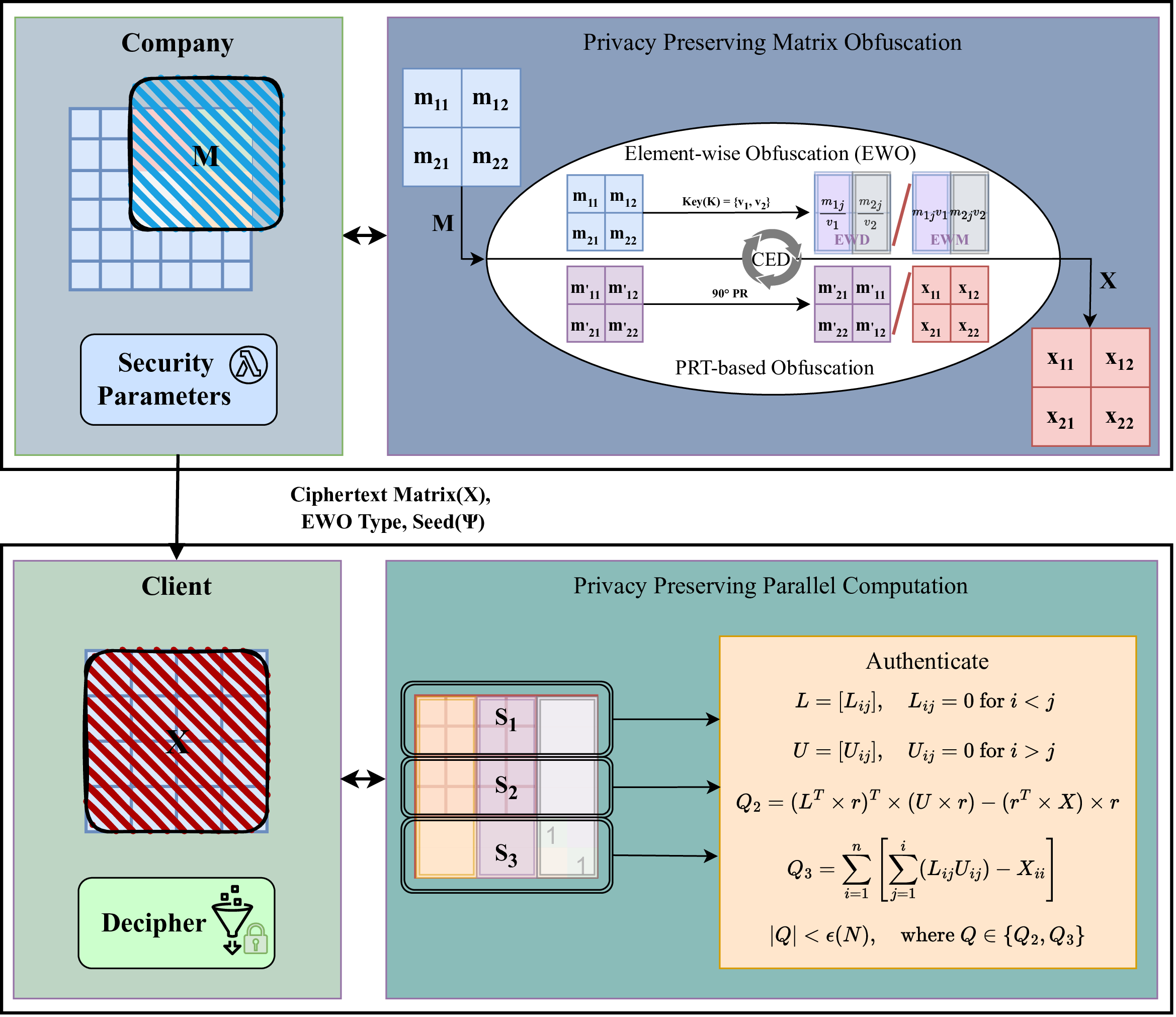
Matrix determinant computation (MDC) is crucial in cryptography, control systems, and machine learning but remains computationally intensive, especially in resource-constrained environments like IoT. Existing privacy-preserving MDC protocols rely on two edge servers, limiting scalability and efficiency in large-scale applications. We propose a novel framework for Privacy-Preserving Parallel MDC utilizing N > 2 distributed edge servers. The framework introduces Composite Element Distortion (CED), a lightweight encryption method that combines Element-wise Obfuscation (EWO) and Panth Rotation Theorem (PRT)-based Obfuscation. Additionally, the Flip Invariance Theorem (FIT) and Zero Sub-Matrix Theorem (ZSM) are introduced to enhance singularity detection without full determinant computation. The framework includes lightweight authentication, decryption, and parallel LU decomposition to reduce computational complexity. Simulation results demonstrate that the proposed solution achieves secure, scalable, and efficient MDC, making it suitable for real-time applications in IoT and other fields.

Request Access

Privacy-preserving collaborative computation is fundamental to modern distributed systems, particularly in privacy-sensitive applications such as federated learning, secure IoT analytics, and healthcare data processing. This paper introduces the Privacy-Preserving Collaborative Scalar Product (PPCSP) framework, a novel solution for securely computing the sum of element-wise products of private vectors across distributed clients in a decentralized network. The framework employs a hierarchical architecture with dynamically assigned roles, including Manager, Captains, and Members, supported by a Coordination Server and a Computation Server. A novel perturbation-based privacy mechanism ensures that neither intermediate results nor the final scalar product can be inferred by any participant, including the Computation Server. Client authentication using Universally Unique Identifier (UUID) and restricted communication protocols further enhance security. The PPCSP Framework is evaluated on its computational efficiency, scalability, verification and privacy-preserving capabilities. Theoretical analysis demonstrates strong privacy guarantees and correctness, while simulations validate the framework's efficiency and scalability in large-scale deployments. The framework significantly reduces communication overhead and enhances flexibility compared to existing methods, making it suitable for real-world distributed systems requiring secure collaborative computation.

Read Full Paper